418 字

2 分钟

IEEE浮点数

2024-04-21

计算机基础

IEEE浮点数#

IEEE浮点数由3个部分表示：

符号位sign
阶位exp
小数部分frac

浮点数类型	符号sign (bit)	阶码exp (bit)	小数部分frac (bit)
float(32 bit)	1	8	23
double(64 bit)	1	11	52

浮点数 $V = (-1)^S \times M \times 2^E$

32位浮点数的数值#

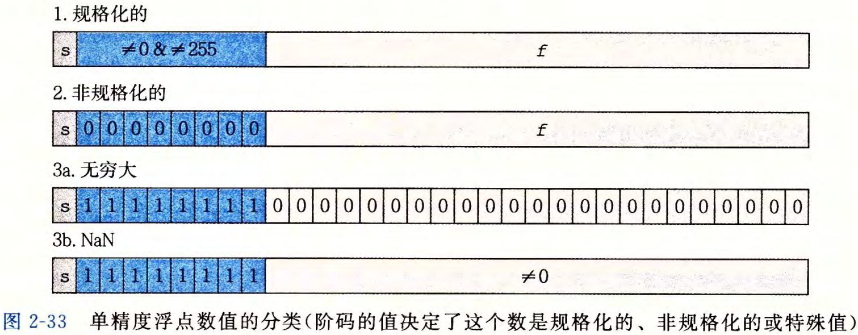
float

如图所示： $V = (-1)^S \times M \times 2^E$
- 蓝色部分为exp阶码
  - 在规格化中，阶码的值为 $E = e - Bias(Bias = 2^{n - 1}) \implies -126 \le Bias \le +127$
  - 非规格化中，阶码的值始终为 $E = 1 - Bias(Bias = 2^{n - 1}) = -126$
- 白色部分f为小数部分
  - 在规格化中，小数部分 $M = 1 + f$ ， $f$ 为小数表示法表示的小数
  - 在非规格化中，小数部分 $M = f$
  小数表示法：如：1011，用小数表示法为 1/2 + 0 + 1/8 + 1/16 = 11/16 = (8+2+1) / 2^4

非规格化数的设计#

非规格化的数，阶码为固定的负数，且f部分为小数表示法，因此非规格化的数整体小于规格化的数，且用于逼近0和表示0.
1. 非规格化数表示的最小正小数为 $\frac{1}{2^{N}}$ (N 表示阶码和小数部分的bit数)
由于非规格化的数阶码固定为 $1 - Bias$ ，因此可以无缝衔接规格化数的最小值。

8位浮点数的数值范围#

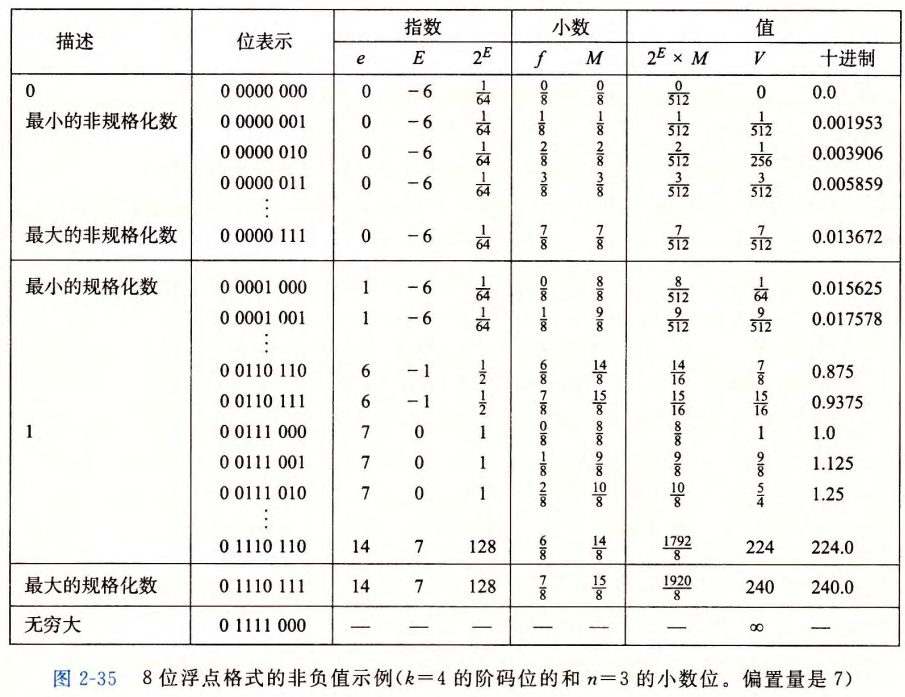
例子：0x4A564504 == 3510593 = 0100 1010 0101 0110 0100 0101 0000 0100
- 每部分的数值：
  - 符号位 $sign = 0$
  - $exp = 10010100 = 148$
  - $f = 101 0110 0100 0101 0000 0100 = 5653764 / 2^{23}$
- 由于是规格化的， $E = e - Bias, M = 1 + f$
- $V = 1 * (1 + 5653764 / 2^{23}) * 2^{(148 - 127)} = ( 1 + 5653764 ÷ 2^{23}) × 2^{21} = 3510593$

IEEE浮点数

https://chrisnake11.github.io/blog/posts/coding/csapp/informationencoding/floatnumber/

作者

Zheyv

发布于

2024-04-21

许可协议

CC BY-NC-SA 4.0

使用Typora编辑博客，并配置Picgo图床自动上传图片