谓词逻辑#
个体变量和谓词#
简单命题 = 主语(独立存在的客体) + 谓语(形容客体性质和客体之间关系的部分)
- 个体词
- 个体常量:表示具体的个体词
- 个体变量:表示泛指的个体词
- 个体域:个体词的取值范围
- 全总个体域:所有个体域构成的个体域。
n元谓词:在非空个体域D上,定义在Dn上的值域为{0, 1}的n元函数,记为P(x1,x2,...,xn);
其中,个体变量x1,x2,...,xn∈D
- 谓词常量:表示具体性质或关系的谓词
- 谓词变量:表示抽象或泛指性质的谓词
谓词中个体词的顺序不能变更。
1元谓词表示一个个体的特性,n元谓词表示n个个体之间的关系。
谓词本身并不是命题,只有用谓词常量和个体常量代替之后才是命题。
谓词逻辑符号化
- 天下乌鸦一般黑;
F(X):x∈crow;G(x,y):x,y are black
则命题符号化为:
(∀x)(∀y)(F(x)∧F(y)→G(x,y))
或¬(∃x)(∃y)(F(x)∧F(y)∧¬G(x,y))
- 每个实数都存在比它大的另外的实数
R(x):x∈R;L(x,y):x<y
则命题符号化为:(∀x)(R(x)→(∃y)(R(y)∧L(x,y)))
谓词公式#
-
常量符号: 个体域D的某个元素
-
变量符号: 个体域D的任意元素
-
函数符号: 在个体域集合内,个体域到另一个个体域个体词的变化。(代替蕴含式),用小写字母表示
-
谓词符号:表示个体域集合内D^n -> {0, 1}的任意一个谓词。用大写字母表示。
-
项:由任意的常量符号或者变量符号通过有限次函数符号组合而成。
合式公式#
-
原子公式:由n元谓词,和项组成的原子谓词。
-
合式公式:由有限个合式公式组合而成。
原子公式是合式公式
联结词连接的合式公式也是合式公式
由量词连接的合式公式也是合式公式
自由变元与约束变元#
- 给定一个公式G,若变元x出现在使用变元的两次的辖域之内,则称变元x的出现为约束出现,此时x称为约束变元。反之称为自由变元。
- 辖域:若量词后有括号,则括号内的子公式就是该量词的辖域。(∀x)(...)
- 没有括号,辖域的范围就是相邻的公式。(∀x)P(x)G(y),y为自由变元。
修改约束变元时,需要修改辖域内的所有约束变元
对于自由变元,应当使用新的符号进行替换。
- 闭式:公式G中没有自由出现的个体变元(都是约束变元),称为封闭的合式公式。
谓词公式的解释#
谓词公式G的解释I由如下四部分组成:
- 非空的个体域集合D
- G中的每个常量符号
- G中的每个n元函数符号,指定由D^n -> D中的某个特定函数。
- G中的每个n元谓词符号,指定由D^n -> {0, 1}
- 举例:

基本等价公式:
- 量词可以任意在辖域的括号内外切换,只影响约束变元。
- 对于同一个谓词公式,多个量词公式的顺序可以交换。
(∀x)(G(x)∧H(x))==(∀x)G(x)∧(∀)H(x)
(∃x)(G(x)∨H(x))==(∃x)G(x)∨(∃x)H(x)
谓词和命题的区别#
- 命题公式:不含量词的公式
- 谓词公式:具有量词的公式
前束范式(量词约束都在前面)#
对于公式G,一切量词都存在于公式的最前端,且量词的辖域都延伸到公式的末端。
(Q1x)(Q2x)...(Qnx)M(x1,x2,...,xn)
其中Qi是量词,M称作公式G的母式或者基式,M中不再存在量词。
- 求解前束范式
- 消去公式中的联结词 ”->”, ”<->”
- 将否定联结词内移到原子谓词公式的前端
- 将量词移动到公式的最前端

疑点解释:
(∀x)(∃y)P(a,x,y)∧(∀x)((∃y)¬Q(y,b)∧¬R(x))
这一步骤:前面的x是全称量词,使用合取可以合并。
(∀x)((∃y)P(a,x,y)∧(∃y)¬Q(y,b)∧¬R(x))
这一步骤:y是存在量词,使用合取不能合并。需要析取才能合并。
全称量词指整个个体域,而存在量词指个体域的一部分,两部分并不相同。
(∀x)((∃y)P(a,x,y)∧(∃y)¬Q(y,b)∧¬R(x))
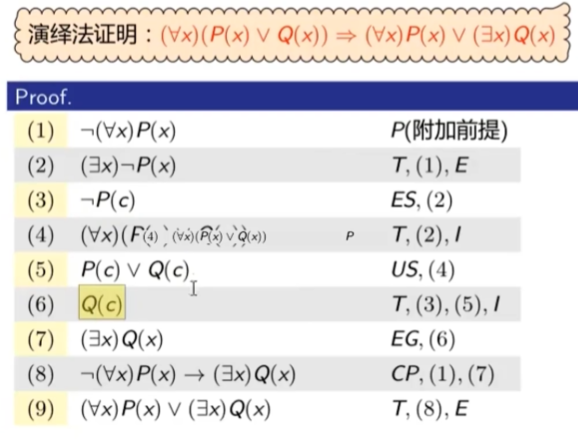
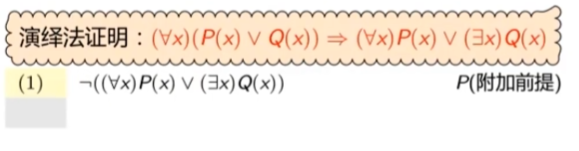
推理规则#
推理形式和推理规则#
设Gn,H是公式,H是G的逻辑结果当且仅当对任意解释I,若I同时满足G_n,则I满足H。记为:G1,G2,...,Gn⟹H,此时称G1,G2,...,Gn⟹H是有效的,否则是无效的。
可以把G1,G2,...,Gn这一组前提(premise)用集合Γ表示。称H为结论(conclusion)。
H是前提集合Γ的逻辑结果Γ⟹H,当且仅当G1∧G2∧...∧Gn→H为有效公式。
推理规律#
I13:(∀x)G(x)∨(∀x)H(x)⟹(∀x)(G(x)∨H(x))
I13:(∃x)G(x)∧(∃x)H(x)⟹(∃x)(G(x)∧H(x))
将个体域缩小
描述整体需要量词,描述个体不需要量词
当需要从整体与个体之间的过渡时,需要消去或添加量词
(∀x)G(x)⟹G(y),y不再G(x)中约束出现
(∀x)G(x)⟹G(c),c为任意个体常量
全称量词 -> 常量变元
全称量词 -> 自由变元
(∃x)G(x)⟹G(c),c为使G(c)为真的特定的个体常量
当G(x)中还有除x之外的自由变元(如:y),使用关于这些变元(y)的函数符号来取代c(如:f(y))
存在量词 -> 自由变元的函数
G(y)⟹(∀x)G(x),G(y)中无变元x
自由变元 -> 全称量词
G(c)⟹(∃x)G(x),c为特定个体常量
或:G(y)⟹(∃x)G(x),G(y)中无变元x
常量变元 -> 存在量词
自由变元 -> 存在量词