关系理论
序偶与笛卡尔积
序偶:两个元素按照一定顺序组成的二元组<x, y>
笛卡尔积:两个集合A, B,,称为集合A和B的笛卡尔积;
笛卡尔积表示两个集合内,分别属于不同集合的每个元素之间存在的的某种关系的集合。
笛卡尔积的性质
- 笛卡尔积不满足交换律
- 当且仅当
- 笛卡尔积不满足结合律;
- 对于两个有限集,
- 笛卡尔积对于并运算和交运算满足分配律
推广
-
n重有序组:将n个元素按照一定次序排列而成的有序n元组
-
笛卡尔积:设有n个集合,则
二元关系
二元关系:两个非空集合A, B,则的任意子集R为从A到B的二元关系。A是前域,B是后域
序偶,记为,读作:x对y有关系R 没有关系,在R上加斜线 /
- A和B的关系数量 =
i元关系数量 =
- ,R为A到B的空关系(empty relation);
- ,R为A到B的全关系(total relation);通常记为
- ,R为A到B的恒等关系(identity relation);
即:x自相关
定义域和值域
本质上函数(function),也是一组二元关系,表示一种多对1的二元关系映射。 设R是A到B的二元关系,A为关系R的前域,B为关系R的后域;
令:
则C为R的定义域(domain),D为R的值域(range),记为
为R的域(field)
推广:n元关系
n个非空集合所对应的笛卡尔积的任意子集R,称作这n个非空集合之间的n元关系
关系表示
-
关系图(有向图)表示法:
- 点:表示集合中的元素
- 有向边:的关系
- 环:自相关
-
矩阵表示法:使用一个关系矩阵表示集合之间的关系(上面的有向图)
- 当矩阵的值为0/1是,为邻接矩阵。
- :集合中第个元素和集合中第个元素的关系
布尔矩阵的运算:
并运算和交运算:对矩阵的对应元素一对一地进行与/或运算。
积运算,对应的行,列元素进行或运算,存在1,的结果为1
关系运算
关系是一种特殊的集合(集合是父类,关系是子类)。因此关系继承了集合的所有运算定律(如:并、交、差、补)。
关系的复合运算
设A, B, C三个集合,R是A到B的关系,S是B到C的关系。
则:R与S的复合关系(合成关系)(composite relation),记为,是A到C的关系。
即:R与S的复合关系就是A到B再到C传递得出关系。对应有向图中由A元素到C元素的路径。
关系的逆运算
对于A到B的关系R,那么B到A的关系叫做R的逆关系,记为:,其中:"" 称作逆运算
- 关系矩阵中,表示为矩阵的转置
- 有向图中,将边调转方向
关系的运算定律
设 表示为集合A恒等关系,包含集合A中所有自己到自己的关系。
- 结合律:
- 同一律:
- 分配律:
- 分配率中,属于同两个集合的关系先∩再运算得到的关系是先运算再∩得到的子集。
- 对于并运算直接相等。
- 逆运算:,路径反向
- 逆运算对于并、交、补不需要换顺序。
关系的幂运算
关系的复合运算()可以满足幂运算。
幂运算收敛定理:
- 求R的n次幂,当达到某一次幂后,结果保持不变(某个非空集合,或者空集)。
关系的性质
-
自反性:对于关系R,对任意的都有,则R在A上是自反的,具有自反性(reflexivity)
每个元素都和自己存在关系
- 有向图:每个点存在自环
- 关系矩阵:对角线全为1
-
反自反性:任意元素都不存在自反性。(antireflexivity)
自反性:如小于等于、同姓、整除 反自反性:小于、父子关系
-
对称性:对任意的xRy,都有yRx
这种关系是相互的
- 关系图:边都是双向的
- 关系矩阵:对称矩阵
-
反对称性:不存在任何一个xRy,都有yRx。
对称:同姓、朋友、同余 反对称:父子、小于等于、包含、整除
- 传递性(transive),顾名思义。
- 关系图:任意一条长路径,都存在直达的路径
- 关系矩阵:根据下标逐个判断
传递性:小于、包含、整除、飞机可达 非传递关系:父子、朋友、婚姻、飞机直达
关系性质的判定定理
- R是自反的,当且仅当
包含I_A的所有元素
- R是反自反的,当且仅当
没有不存在I_A的元素
- R是对称的,当且仅当
- R是反对称的,当且仅当
- R是传递的,当且仅当
关系性质的保守性
- 如图

对于逆运算和交运算,能够保持原来的性质 并运算不能保证反对称和传递 复合运算只有自反性 补运算只能保证反自反、对称、反对称
关系的闭包
闭包(closure)问题:给给定的关系中添加最少的元素,使其具有需要的特殊性质。
设R是集合A上的关系,存在A上的另一个关系R’,满足:
- R’ 是自反的(对称的、传递的)
- 对任何自反的(对称的、传递的)关系R”,如果R R”,就有R’ R”,则称R’ 是 R的自反闭包(reflexive closure)(对称闭包(symmetric closure)、传递闭包(transitive closure)),记为r(R),s(R),t(R)
R的性质不清楚,但是加上R’后就得到一个特殊性质的R”
闭包的求解
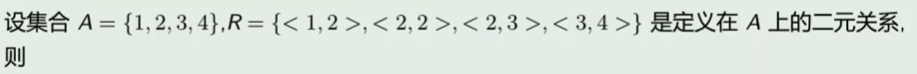
- 对于自反闭包:补上自己到自己的关系
- 对于对称闭包:补上相互的关系
- 对于传递闭包:补上长路径(路径长度 >= 2)上的直接路径
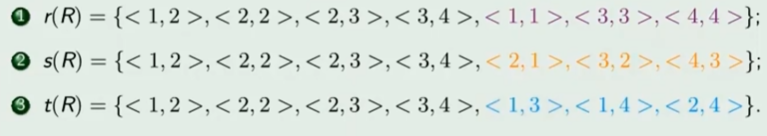
关系运算求闭包
- 例子

