等价关系(分类问题)
非空集合A上的关系R,满足自反性、对称性、传递性。则R是A上的等价关系;
同姓关系、等于关系。 朋友关系(不存在传递性),包含关系(不对称)
- 有向图:每个元素都有自环、每个点之间都是双向边、每个长路径都有直达路径。
- 关系矩阵:对角线全为1,矩阵是对称的,k[i][j],存在a[x][j] b[i][x]
同余关系(等价关系):
- 自反性:x % x == x % x;
- 对称性:x % y == y % x;
- 传递性:x % y % z == x % z;
mod,(x - y) | y(x - y 能整除 y)
等价类
设R是非空集合A上的等价关系,对于任意的,称集合,为x关于R的等价类(equivalence class)x为[x]_R的生成元(generator)
等价关系中,由某个元素为第一元素(生成元),得到的第二元素集合(等价类)。

- 等价类是非空的
- 对任意的,如果,则有,否则
商集
由等价关系R确定的一切等价类的集合,称为集合A上关于R的商集(quotient set),记为A/R,即:
等价类(集合)的集合
等价类可用于:分组的报文转发、软件测试项目的分类、商品促销的分类
即:将二元关系,按照第一元素进行分类
集合
对于给定非空集合A,对于集合的集合满足
- π的元素都是A的子集
- π的每个元素互不相交,。
- π的所有元素,构成了A,
那么:集合π就是集合A的一个划分(partition),π中的集合元素叫做划分的块(block)或者类(class)
等价划分
对于非空集合A上的等价关系R,商集A/R就是A的一个划分。叫做由R所导出的等价划分。
一个集合有多重划分,不同的等价关系能导出不同的划分。
集合划分 -> 等价关系
给定集合A的一个划分,则由该划分确定的关系
是A上的等价关系。
关系R就是由划分π所导出的等价关系。
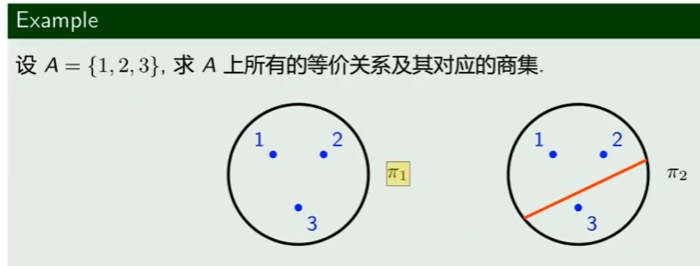
列举出所有划分方式,采用定理得出每一种划分对应的等价关系以及商集。
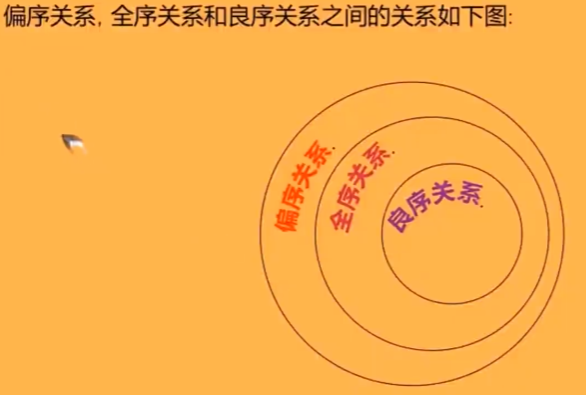
偏序关系(排序问题)
设R是非空集合A上的关系,如果R是自反的、反对称的、传递的,那么R是集合A上的偏序关系(partial order relation)
记为 ,并将,记为,
序偶:,称为偏序集(partial order set)
- 关系图的体现:
- 自反:每个结点都有自环
- 反对称:结点之间的有向边只有一条
- 传递的:任意长路径都有直达的路径
偏序关系是一种泛指的关系,不仅仅局限于小于等于关系。
可比、覆盖
对于非空集合A上的偏序关系R,A的任意两个元素x, y
- 如果 x <= y 或 y <= x,则x与y可比
- 如果 x <= y 且 不存在 使得 x <= z <= y,则 y 覆盖 x
覆盖,不存在中间元素

哈斯图
将有向关系图,简化得到的图叫做哈斯图。
- 取消结点的自环
- 取消传递性得到的边
- 将有向边向上,去掉箭头。(起点在下方,终点在上方)。
最大元和最小元
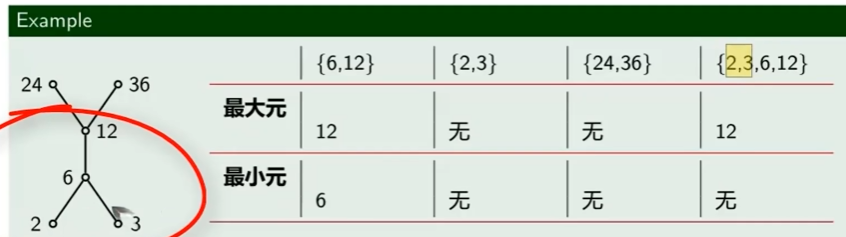
2、3不是最小元,而是极小元
极大元和极小元
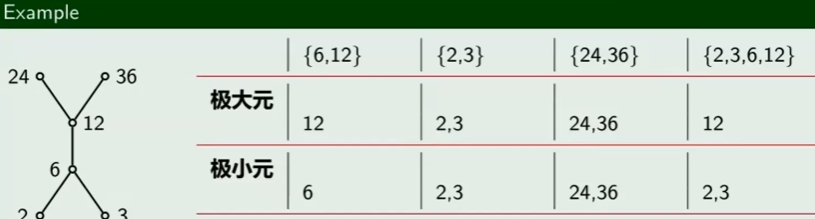

最大/小元,和其他元素都可比 极大/小元,存在不可比的元素
上界和上确界
设<A, <=> 是偏序集,B是A的任意一个子集。
如果存在,使得
- 对任意的满足 x <= a,则a为B的上界
上界:父集合A中 大于等于 B的最大元 的元素
- 若是B的上界,且元素是B的任何一个上界,若均有,称a’ 为 B的最小上界或上确界
上确界:上界中的最小值(唯一)(直接上界)。
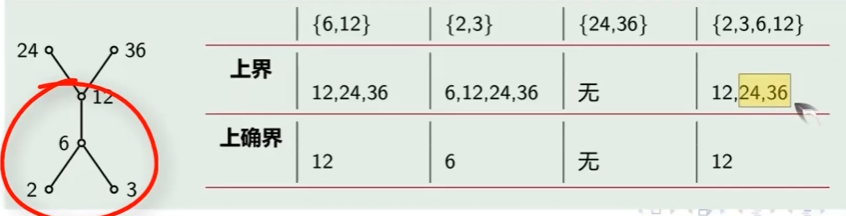
下界和下确界
同理可得
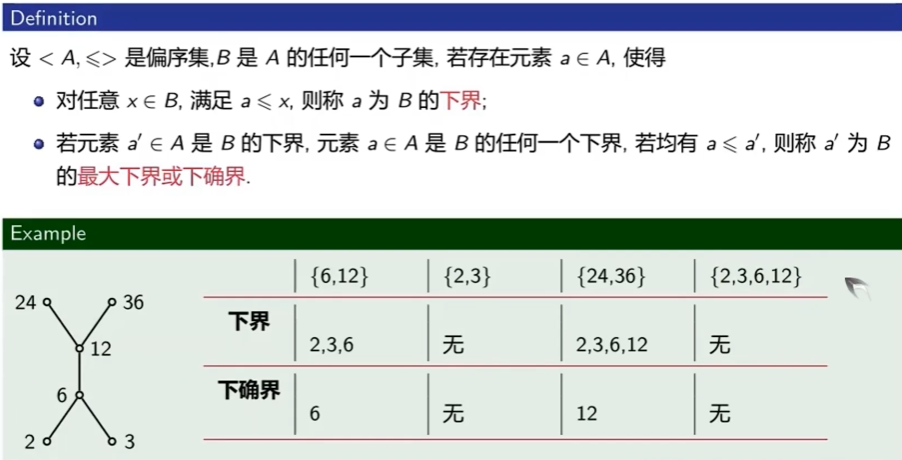
上下界和上下确界在A中寻找
上下界不一定存在,存在可能是多个
上下确界不一定存在,存在必唯一
存在上下确界,必存在上下界
拟序关系
非空集合A上的关系R,是反自反、传递的、反对称,叫做拟序关系;记作"";
序偶<a, < >称为拟序集(quasi-order set)
如:实数内的小于关系、幂集上的真包含关系
全序关系
在偏序关系R内,集合A中的任意两个元素都是可比的,则偏序关系R也叫做全序关系
序偶叫做全序集(total order set),或线序集、链
在哈斯图上,全序关系的图像为一条链。
良序关系
设 是一个全序集,任何A的非空子集都有最小元素。
则""称为良序关系(well order relation),此时 称为良序集(well order set)
整数集上的小于等于不是良序关系,但是正整数集上的小于等于是良序关系
良序关系一定是全序关系
有限全序集一定是良序集
良序定理
所有集合都可以良序排序,即:存在一种方法实现良序排序。
偏序关系、全序关系、良序关系