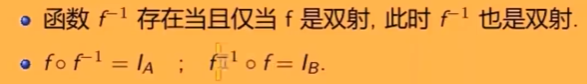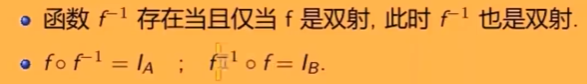628 字

3 分钟

函数

2024-04-18

离散数学

函数#

设 $f$ 是集合 $A$ 到 $B$ 的关系，如果对每个 $x \in A$ 都存在唯一的 $y \in B$ ，使得 $<x , y> \in f$ ，

每个x必须有对应的y x 和 y 只能是1对1 或者多对1的关系

则称关系 $f$ 是 $A$ 到 $B$ 的函数或者映射。

记为 $f: A \rightarrow B$ ，A为函数的定义域，记为 $domf = A;f(A)$ 为函数的值域，记为 $ranf$

记，所有 $A$ 到 $B$ 的一切函数构成的集合： $B^A = \{ f | f : A \rightarrow B \}$

$f: A \rightarrow B$ ，对于每个A都可以对应|B|中元素的一个，遍历所有A的元素，一共有 $|B|^{|A|}$ 种选法。

关系和函数
- 种类数量不同，A到B的关系有 $2^{|A| \times |B|}$ 个，而函数只有 $|B|^{|A|}$
- 基数不同，关系的基数可以为 $|A| \times |B|$ ，而函数的基数只能为 $|A|$
- 第一元素不同：函数的第一元素不能重复。

函数类型#

单射： $\forall x_1 \in A, \forall x_2 \in A, if \space x_1 \neq x_2, then \space f(x_1) \neq f(x_2)$

$|A| \leq |B|$

$|A| \geq |B|$

满射也就是每个x都对应一个y，且都是1对1的关系。

要求： $|A| = |B|$

函数可视为一种特殊的二元关系

设 $f: A \rightarrow B, g: B \rightarrow C$ 是两个函数

则f与g的复合关系可以表示为：

$f \circ g = \{ <x, z> | x \in A, z \in C, \exist y \in B \to ( y = f(x) \and z = g(y)) \}$

表示为A 到 C的函数，称为f与g的复合函数(composition function)

记为: $f \circ g : A \rightarrow B$

复合函数的前提条件： $ranf \subseteq domg$

$dom(f\circ g) = domf, ran(f \circ g) \subseteq rang$

交换之后，值域和定义域的映射顺序改变了。

设 $f: A \rightarrow B$ 是函数

如果 $f^{-1} = {<y, x> | x \in A, y \in B, y = f(x)}$ ，是从B到A的函数

则 $f^{-1}: B \rightarrow A$ 为函数 $f$ 的逆函数

函数

作者

Zheyv

发布于

2024-04-18

许可协议