777 字
4 分钟
图论
图论
图的定义
无序对和无序积
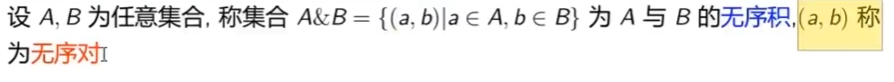
与序偶不同,

图的定义

图的表示
- 图形表示法(画图)
- 集合表示法(使用序偶和无序对)
- 邻接矩阵表示
邻接矩阵的假设:有限图:只有一条边
补充:
- 邻接表表示法
- 十字链表法
图的分类
- 无向图、有向图、混合图
- 多重图、线图(线性的)、简单图(无环)
- 赋权图、无权图
子图和补图
-
子图:边和结点都是包含关系。
- 真子图:不相等
- 生成子图:V相等,E为包含关系
- 最小生成子图:权值最小的生成子图。
- 导出子图:V为包含关系,E为对应的所有边。
如全校关系网络图中,提取某个班的导出子图
-
完全图:在简单图中,任意两个结点都有边相连
- 无向完全图、有向完全图
没有自环,邻接矩阵对角线为0
- 无向完全图、有向完全图
-
补图:完全图的边 - 简单图的边 = 这个简单图的补图
不要漏掉补图中的孤立结点
握手定理
- 结点的度:…
- 度为1的结点叫做悬挂结点,对应的边为悬挂边
- 最大入/出度:所有结点中,单个结点的最大入/出度。
握手定理:
推论:度数为奇数的结点个数为偶数。
图的同构
设有两个图G和G’,如果存在结点V的双射函数,任意两点之间的边都相同,且重数也相同,则称图G和图G’同构(isomorphism)

不同构的判断方法
- 通过必要条件判断(用于判断不同构)
- 结点数目相同
- 边数目相同
- 同一度的结点数相同
连通图
通路:由结点和边相继交错出现的序列。
边的数量为通路的长度,为通路的端点。当v_0 = v_k时称作回路。
通路的边互不相同,叫做简单通路
回路的边互不相同,叫做简单回路,反之为复杂回路。
点和边都不相同叫做基本通路/回路
回路是通路的特殊情况。
- 线图中,长度为m的通路数量:
- 设A的为图G的邻接矩阵。中,表示从i -> j 长度为m的路径数量
- 矩阵总和为,整个图中长度为m的通路数量。
可达性和最短通路(最短路径)
可达关系判定定理

计算所有可能长度的通路((结点的数量))。如果存在就可达。
无向图的可达矩阵是对称的,有向图不对称。
- 短程线:最短通路
连通图
- 弱连通图:任意一对结点,至少单方面可达。
- 强连通图:任意一对结点,相互可达。
- 强连通图的充分必要条件:存在一条经过所有结点的回路。
- 可达性矩阵全为1。
- 单项连通图的可达矩阵P,除对角线外,均为1 +
