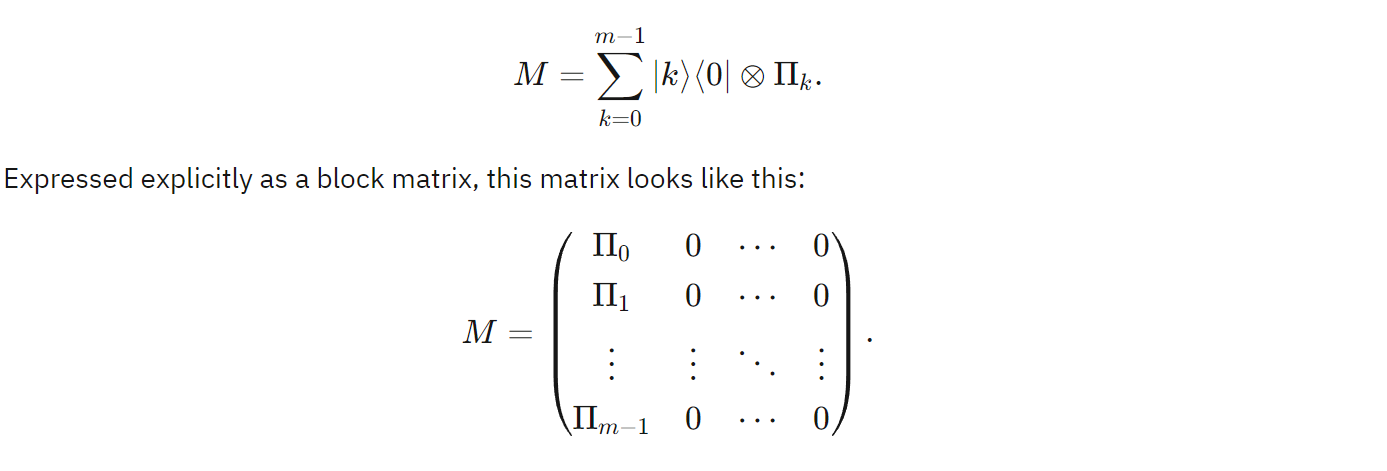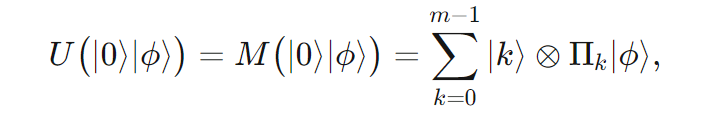Multiple System#
在认识Quantum Information之前,我们需要先了解多系统这个概念。
对于任意一个单个的系统X,可能存在a∈Σ的任意一个状态。这时候如果有另外一个系统Y,Y可能是b∈Γ的任意一个状态。
任意多个的单个系统,我们可以通过将其看作为单个系统。方法如下,一个系统必定存在一个对应的状态,假设存在2个系统XY,无论这两个系统是否相关,如果把这两个系统视作一个系统,那么在某一时刻必定有一个对应的状态,这个状态可以用X和Y各自的状态来表示。即:(X,Y)的状态为{(a,b)∣a∈Σ,b∈Γ},这个单一系统的状态集合表示为子系统状态集合的笛卡尔积(Cartesian Product)。
继续拓展为任意多个系统可以得到:
(X0,X1,...,Xn−1)Σ1×...×Σn={(a1,...,an)∣a1∈Σ1,...,an∈Σn}其中(X0,X1,...,Xn−1)看作n个单个系统合并成的单个系统。这个系统的状态属于下面的集合。
多系统和串#
通过这个多系统的概念,可以推导出串这一数据结构。把串看作一个多系统,串的每个位置就是单个系统,每个系统的状态集合是相同的(当然也可以不同)。
如:一个比特数据流就是一个01串,每个系统的状态为0或1,集合的数量为比特数量。字符串也是一种特殊的串,单个系统状态的集合与比特数据流不同。
Σ1=Σ2=...=Σn={0,1}Σ1×Σ2×...×Σn={0,1}n上面的集合是一个长度为n的比特数据流系统的状态集合。每个单系统的状态集合都是{0,1}
Quantum Infomaton#
对于一个量子态,我们可以看作为多个量子比特组合成的复合系统。
一个量子态可以由一个列向量来表示,每个元素为量子态的每个基态的概率幅(复数complex number),且这个向量的欧几里得范数等于1.
如一个2量子比特的量子态,使用Dirac Notation(狄拉克表示法),可以表示为:
∣ψ⟩=21∣00⟩+21∣11⟩我们同样可以使用一个向量来表示这个量子态
∣ψ⟩=21(10)⊗(10)+21(01)⊗(01)=211000+210001=210021
在进行量子相关的代数运算时(如使用矩阵进行操作),使用Dirac Notation不一定是表示量子态的最佳选择,要灵活运用。
叠加态(Product State)#
任意两个量子态之间的张量积得到一个新的量子态,张量积表示为⊗,说明这两个向量之间互不相关(nothing to do with another),组成的新的量子态可以表示为∣ϕ⟩⊗∣ψ⟩,新的量子态的概率幅的欧几里得范数仍然为1.
互不相关:测量其中一个量子态坍缩后,并不影响第二个量子态坍缩各个基态的概率。
纠缠态(Entangled State)#
纠缠(entanglement)可以看作为相关(correlation),对于两个纠缠的量子,测量其中一个量子,会影响到另外一个量子的概率幅。
纠缠-叠加,等价于 不相关-相关。
无论是哪种量子态,概率幅的欧几里得范数必定为1.
区分叠加态和纠缠态#
假设存在一个2量子比特的量子态。为了区分这两个量子比特是叠加态还是纠缠态,需要将这个量子态拆分为两个单量子的量子态的乘积形式
如果成拆成
(32∣0⟩+35∣1⟩)⊗(21∣0⟩+21∣1⟩)两个单量子量子态的张量积形式,说明这个两个量子态是叠加态。
如果只能够得到如下的形式:
∣0⟩⊗(43∣0⟩−21∣1⟩)+∣1⟩⊗(2i∣0⟩+21∣1⟩)两个双量子量子态相加的形式,说明这两个量子处于纠缠态。
测量量子态(Measurements of quantum states)#
测量一个量子态,坍缩为某个基态∣a⟩的概率,从数学上可以表示为一个即将坍缩的基态与量子态向量的内积的平方:∣⟨a∣ψ⟩∣2
量子态的部分测量#
上面的情况介绍了量子态整体坍缩为某一个基态的情况发生的概率。但是在实际的量子算法中,我们往往需要量子态中的部分量子(即:量子态的一部分)。
假设存在一个2量子的量子态,其中第一个量子态测量结果为∣a⟩
∣ψ⟩=a∈Σ∑∣a⟩⊗∣ϕa⟩where:∣ϕa⟩=b∈Γ∑αab∣b⟩剩下的向量∣ϕa⟩需要经过归一化之后才能表示真正的量子态。
∣∣∣ϕa⟩∣∣∣ϕa⟩∣∣∣ϕa⟩∣∣=b∈Γ∑∣αab∣2表示为:当第一个量子态测量为∣a⟩时,量子态会坍缩为如下的形式。
∣∣∣ϕa⟩∣∣∣ϕa⟩例如:对于如下的双量子量子态。
∣ψ⟩=21∣00⟩−61∣01⟩+6i∣10⟩+61∣11⟩可以化简为如下的形式:
∣ψ⟩=∣0⟩⊗(43∣0⟩−21∣1⟩)+∣1⟩⊗(2i∣0⟩+21∣1⟩)当第一个量子测量为∣0⟩或∣1⟩时,量子态会分别坍缩为后面括号中的状态。
酉变换(Unitary Operations)#
酉矩阵的定义:对于一个元素为复数(complex number)的方阵U,满足如下条件。
UU†=U†U=IU†表示U的共轭转置(conjugate transpose),即:将矩阵中所有复数的虚部取反
,然后再进行转置操作。
U†=UT根据定义可以推出,如果U是酉矩阵,那么U的共轭转置等于U的逆
U†=U−1常见的Hardmard gate,单位矩阵都是酉矩阵,且酉矩阵的张量积(如:H⊗I)也是酉矩阵。
H=[212121−21],I=[1001]但是不是所有的酉变换都可以经过酉矩阵的张量积得到,SWAP和CNOT就无法通过酉矩阵的张量积得到,但是这两个都是酉变换。
SWAP=1000001001000001SWAP的作用,如果是∣01⟩或∣01⟩量子态,交换前后两个量子。也可理解为直接交换这两种量子态。
观察逻辑门的作用可以直接观察逻辑门矩阵的列向量所表示的量子态结构。
这里第一列为1000对应∣00⟩,保持不变,第二列由∣01⟩变为了∣10⟩表示的向量,第三列由∣10⟩变为了∣01⟩表示的向量,第四列同理保持不变。
CNOT=1000010000010010CNOT矩阵的作用:如果第一个量子是1,第二个量子取反。
CNOT(Controlled-NOT)矩阵的右下角是一个NOT矩阵,这个NOT可以改成其他的变化矩阵, X, Z, SWAP矩阵都可以。这一类矩阵称之为CU矩阵。
任意的投影测量可以用U矩阵、基本基测量、以及额外的空间来实现。#
利用额外的空间,来实现同时保存测量的结果以及每个结果的概率幅。
假设Π0,Π1,...,Πm−1是关于X的投影矩阵。我们假设存在同样的量子态为Y,他的初始态为∣0⟩,
Y可以使用以下的矩阵M来测量,结果与X的结果集相同。
首先考虑这个矩阵M,能够用于测量(Y, X)系统中,Y的一部分。
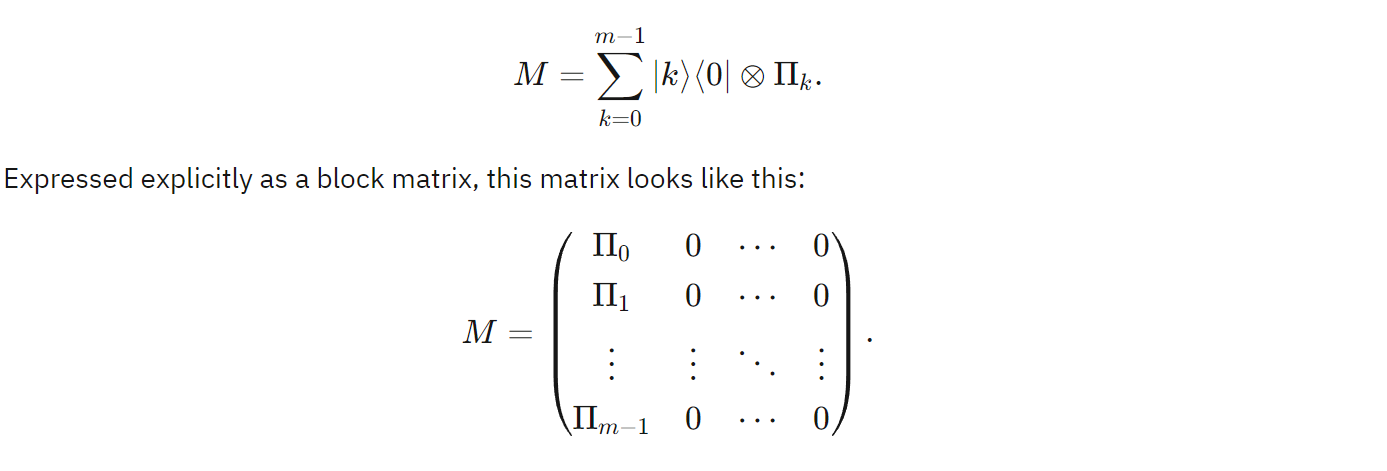
矩阵M的前m个列向量是正交的。但是矩阵M不是Unitary Matrix,因此无法测量整个(Y, X),把M中的0元素替换,使得M变成一个Unitary Matrix。
使用以下的矩阵U对这个系统进行测量:

假设:∣0⟩,∣ϕ⟩分别为(Y, X)的量子态。使用矩阵M进行变换。∣k⟩表示序号为k的测量结果。
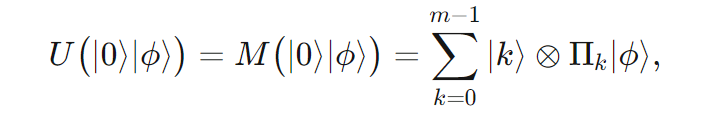
矩阵U相比于投影矩阵Π使用了更多的空间,但是经过U(Y,X),我们可以同时得到X测量结果的拷贝,以及每个结果的概率。