- 1. 量子电路基础(直接构建简单的量子电路)
- 2. 梯度和训练
- 3. 测量
- 4.Dynamic Circuit(根据测量结果,动态调整电路)
- 5. 线路模板
- 6. 自定义模板
- 7. 查看量子电路
- 8. 编译量子电路
- 9. 量子编译流程
- 10. 使用CUDA Quantum
1. 量子电路基础(直接构建简单的量子电路)
PennyLane主要有2个部分组成: device,qnode
device:表示运行的量子设备
shots_list = [5, 10, 1000]dev = qml.device('default.qubit', wires=['aux', 'q1', 'q2'], shot=shot_list)- 第一个参数为device的类型。
- 第二个参数为量子比特数量,也可以使用标签数组对每个比特进行标记。一个wire表示一个比特
- 第三个参数为测量的次数列表,用频率来拟合概率。如果为空,就直接计算精确的概率辐。
qnode:表示一个量子逻辑电路,在QNode中定义了circuit function,即:量子逻辑电路。
@qml.qnode(dev) # 使用decorator更方便地给QNode指定devicedef my_quantum_function(x, y): qml.RZ(x, wires='q1') qml.CNOT(wires=['aux' ,'q1']) qml.RY(y, wires='q2') return qml.expval(qml.PauliZ('q2'))draw()可以使用字符直接绘制量子电路
circuit = qml.QNode(my_quantum_function, dev)print(qml.draw(circuit))也可调用matplotlib包,使用draw_mpl()来绘制更清晰的电路图。
import matplotlib.pyplot as pltqml.drawer.use_style("black_white")fig, ax = qml.draw_mpl(circuit)plt.show()参数传播机制:
在QNode中,参数的传播是并行的,即对于单独的一个QNode中的所有参数以ndarray的形式,并行执行。(类似于在机器学习中对一批参数应用一个函数)
对于(最多)中等大小的量子线路(≲20 条量子线)和中等数量的参数(≲200 个)在经典模拟器上执行的情况下,通常可以从广播中受益。
从其他软件导入量子电路
Pennylane可以从其他的量子电路相关软件(如:Qiskit)导入量子电路。
前提:需要安装对应的软件包(如:PennyLane-Qiskit)
2. 梯度和训练
Pennylane通过一个自动微分的API,与其他经典的神经网络框架结合(如:Numpy、PyTorch、TensorFlow等。),让其他的神经网络框架可以像训练经典神经网络一样,训练量子电路。
在构建device时,通过参数interface可以指定自动微分的框架。
@qml.qnode(dev, interface="torch") # 使用PyTorch作为微分框架def my_quantum_circuit(...): ...当使用标准的Numpy框架时,Pennylane提供了一些内置的优化器进行优化。
如果使用的是Pytorch,通过调用torch的相关API,可以将经典数据直接传递给QNode,同时torch可以直接获取QNode的梯度,使用torch中的优化器优化混合量子电路。
2.1 自定义梯度下降方法
要想使用CustomFunction作为自定义的梯度梯度下降方法,需要使用apply()方法。
class CustomFunction(torch.autograd.Function): # CustomFunction继承自torch.autograd.Function @staticmethod def forward(ctx, x, exponent=2): ctx.saved_info = {'x': x, 'exponent': exponent} return x ** exponent
@staticmethod def backward(ctx, dy): x = ctx.saved_info['x'] exponent = ctx.saved_info['exponent'] print(f"Calculating the gradient with x={x}, dy={dy}, exponent={exponent}") return dy * exponent * x ** (exponent-1), None测试结果如下:
val = torch.tensor(2.0, requires_grad=True)res = CustomFunction.apply(val)res.backward()val.gradCustomFunction函数的输入输出都是拉平后的一维数据。
2.2 Pennylane的梯度计算方法
Pennylane设计了两种方法计算梯度
-
基于模拟的微分。当使用量子仿真模拟时,可以直接使用经典的反向传播算法来计算梯度。
-
硬件兼容的微分。一般可以使用
parameter-shift参数偏移和finite-diff有限差分的方法计算。
基于
Hardmard-Test的梯度估计?
device()中的diff_method可以指定梯度计算的方法。默认为diff_method=best,Pennylane将根据device和interface自动选择最优的方法。
@qml.qnode(dev, interface='torch', diff_method='parameter-shift')def circuit(x): qml.RX(x, wires=0) return qml.probs(wires=0)2.3 交给Torch训练
除了直接对Quantum Circuit自动微分。Pennylane还提供了更高级的API.
如果设计的QNode可以被Torch兼容,那么QNode可以使用qml.qnn.TorchLayer()直接转化为torch.nn的经典层,直接进行训练。
3. 测量
使用qml.expval(op)可以在测量前应用一个operation。
下面的例子在测量前使用Pauli—Z门。用于测量本征态。
def my_quantum_function(x, y): qml.RZ(x, wires=0) qml.CNOT(wires=[0, 1]) qml.RY(y, wires=1) return qml.expval(qml.PauliZ(1))4.Dynamic Circuit(根据测量结果,动态调整电路)
Mid-circuit measurements:中段电路测量,根据量子态部分的测量结果,后续执行不同的量子逻辑电路。
在测量后,可以把对应线路归零,重新使用。
postselecting mid-circuit measurements:根据测量结果抛弃(筛选)部分样本。
conditional operators:使用测量的结果,进行条件逻辑判断。
对于部分获得量子态统计数据的api,如:counts(), expval(), probs()等,可以使用参数来获取满足特定测量结果的样本的统计数据。
4.1 测量的实现

- 延迟测量(Deferred measurements)
延迟测量支持反向传播和有限差分的方法计算梯度,如果postselect没有被使用,则无法使用参数偏移的方法。
- 动态单词测量(Dynamic one-shot)
- 树型遍历(Tree-traversal)
后两种,对于postselect如果被选择,一定会使用参数移位的梯度计算方法。当使用了条件操作符,则只能使用有限差分的方法计算梯度。
这三种技术的优点和缺点差别很大,一般来说:
- 动态一次性采样在多次测量、少量采样的模式下表现出色,
- 树遍历技术可以处理具有大量样本和多次测量的大规模模拟
- 延迟测量是一种通用解决方案,可以在(几乎)所有情况下实现电路中段测量支持,但内存成本较高。它是唯一支持数值解析的方法。
4.2 延迟测量
当使用延迟测量,会给每个mid-circuit measurements添加一个辅助量子比特。 随着量子比特的增加,内存和模拟时长将会指数增长。
把原始的中间测量比特作为控制位,对辅助比特使用CNOT门,再让辅助比特控制后续的电路。 最后延迟测量时,只需要根据辅助比特的结果来判断。
deferred_qnode = qml.defer_measurements(my_qnode)pars = np.array([0.643, 0.246])deferred_qnode(*pars)
print(qml.draw(my_qnode)(*pars)) # 原始mid-circuit测量print(qml.draw(deferred_qnode)(*pars)) # deffered measurement注意:每一次mid-circuit measurement都会添加一个额外的辅助量子比特。
Postselectionwith deferred measurements is only supported onDefaultQubit.
4.3 单次测量
指直接一次完成量子系统的测量,测量结束后,量子态会坍缩到本征态。 测量后不可逆,无法使用本征态验证原始的量子态。
4.4 树形遍历
结合了单次测量内存开销低和延迟测量中采样效率的优点。
4.5 代码示例
dev = qml.device("default.qubit", wires=3, shots=10)
def circ(): qml.Hadamard(0) m_0 = qml.measure(0, postselect=1) return qml.sample(qml.PauliZ(0))
# 通过参数配置QNodefill_shots = qml.QNode(circ, dev, mcm_method="one-shot", postselect_mode="fill-shots")hw_like = qml.QNode(circ, dev, mcm_method="one-shot", postselect_mode="hw-like")5. 线路模板
5.1 SimplifiedTwoDesign
由Cincio 2021等人 提出的一种逻辑门结构,有助于缓解barren plateau现象。
首先是一层RY门,之后使用CZ门和RY门进行操作。
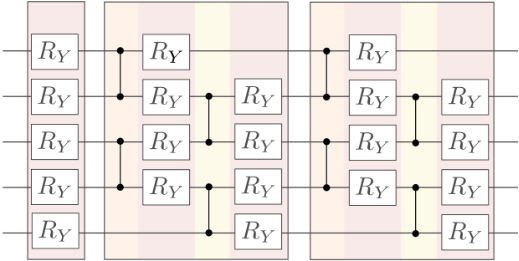
CZ门可以将两个基向量变为最大的
5.2 Broadcasting function
将一个固定的M量子比特逻辑门,以特定的模式(single, double, pyramid, circle等)添加到量子线路中。
注意:
qml.Broadcasting从v0.40开始不推荐使用。建议使用for循环。
5.3 参数初始化
利用模板本身的函数shape()可以获取权重参数的维度大小。
从而直接使用random()初始化参数。
import pennylane as qmlfrom pennylane.templates import BasicEntanglerLayersfrom pennylane import numpy as np
n_wires = 3dev = qml.device('default.qubit', wires=n_wires)
@qml.qnode(dev)def circuit(weights1,weights2): BasicEntanglerLayers(weights=weights1, wires=range(n_wires)) BasicEntanglerLayers(weights=weights2, wires=range(n_wires)) return qml.expval(qml.PauliZ(0))
# 读取编码层的形状shape = BasicEntanglerLayers.shape(n_layers=2, n_wires=n_wires)
# 初始化BasicEntanglerLayers的参数np.random.seed(42) # to make the result reproducibleweights1 = np.random.random(size=shape)weights2 = np.random.random(size=shape)
# 输入对应模块的参数# 如果有多个模板可以添加参数circuit(weights1, weights2)6. 自定义模板
可以自定义一个线路电路,作为自己的模板。
模板只需要逻辑门参数列表和量子比特作为参数。
模板函数内部为一系列量子逻辑门。
from pennylane import numpy as np
def MyTemplate(a, b, wires): c = np.sin(a) + b qml.RX(c, wires=wires[0])
n_wires = 3dev = qml.device('default.qubit', wires=n_wires)
@qml.qnode(dev)def circuit(a, b): MyTemplate(a, b, wires=range(n_wires)) return qml.expval(qml.PauliZ(0))7. 查看量子电路
7.1 查看量子电路的详细信息
qml.spec()方法,可以将QNode类作为参数,返回一个关于量子电路参数的函数spec_func()
这个函数的参数与QNode参数相同,返回的是基于参数构造的量子电路的详细信息。
dev = qml.device('default.qubit', wires=4)
@qml.qnode(dev, diff_method='parameter-shift')def circuit(x, y): qml.RX(x[0], wires=0) qml.Toffoli(wires=(0, 1, 2)) qml.CRY(x[1], wires=(0, 1)) qml.Rot(x[2], x[3], y, wires=0) return qml.expval(qml.Z(0)), qml.expval(qml.X(1))7.2 可视化量子电路
qml.draw_mpl(circuit)(args)可以用于可视化量子电路。circuit为电路模板,args为对应的参数。
dev = qml.device('default.qubit')
@qml.qnode(dev)def circuit(x, z): qml.QFT(wires=(0,1,2,3)) qml.IsingXX(1.234, wires=(0,2)) qml.Toffoli(wires=(0,1,2)) mcm = qml.measure(1) mcm_out = qml.measure(2) qml.CSWAP(wires=(0,2,3)) qml.RX(x, wires=0) qml.cond(mcm, qml.RY)(np.pi / 4, wires=3) qml.CRZ(z, wires=(3,0)) return qml.expval(qml.Z(0)), qml.probs(op=mcm_out)
fig, ax = qml.draw_mpl(circuit)(1.2345,1.2345)fig.show()7.3 利用mid-circuit来debug
qml.Snapshot()方法的使用方法类似于一个gate作用在一个circuit中,但它的作用是存储当前状态下的量子态。
对于不同的模拟设备,存储的数据结构也不同:
- default.qubit:存储为量子态的向量
- default.mixed:存储为密度矩阵的形式
- default.gaussian:存储为协方差矩阵和均方差向量。
dev = qml.device("default.qubit", wires=2)
@qml.qnode(dev, interface=None)def circuit(): qml.Snapshot(measurement=qml.expval(qml.Z(0))) qml.Hadamard(wires=0) qml.Snapshot("very_important_state") qml.CNOT(wires=[0, 1]) qml.Snapshot() return qml.expval(qml.X(0))当直接运行电路时,会忽略Snapshot(),只有使用qml.snapshot()方法运行circuit才会得到中间的量子态。
qml.snapshots(circuit)()注意区分
qml.Snapshot()和qml.snapshot()
debugging
pennylane还提供了类似于gdb的debugging程序,详细见qml.debugging
8. 编译量子电路
量子电路的“编译”,是指将一个给定的量子电路函数、或者量子逻辑门,转化为其他的类型的量子电路。例如:将一个大型的量子逻辑门组成的量子电路,转化为由多个小型逻辑门组成的量子电路。
8.1 电路简化
qml.simplify()方法将量子逻辑门作为参数,能够把这个逻辑门进行简化处理。
>>> qml.simplify(qml.RX(4*np.pi+0.1, 0 ))RX(0.09999999999999964, wires=[0])>>> qml.simplify(qml.adjoint(qml.RX(1.23, 0)))RX(11.336370614359172, wires=[0])>>> qml.simplify(qml.ops.Pow(qml.RX(1, 0), 3))RX(3.0, wires=[0])>>> qml.simplify(qml.sum(qml.Y(3), qml.Y(3)))2.0 * Y(3)>>> qml.simplify(qml.RX(1, 0) @ qml.RX(1, 0))RX(2.0, wires=[0])>>> qml.simplify(qml.prod(qml.X(0), qml.Z(0)))-1j * Y(0)除了简化逻辑门,还可以用于简化一个QNode对象。
dev = qml.device("default.qubit", wires=2)
@qml.simplify@qml.qnode(dev)def circuit(x): ( qml.RX(x[0], wires=0) @ qml.RY(x[1], wires=1) @ qml.RZ(x[2], wires=2) @ qml.RX(-1, wires=0) @ qml.RY(-2, wires=1) @ qml.RZ(2, wires=2) ) return qml.probs([0, 1, 2])输出结果:
>>> x = [1, 2, 3]>>> print(qml.draw(circuit)(x))0: ───────────┤ ╭Probs1: ───────────┤ ├Probs2: ──RZ(5.00)─┤ ╰Probs8.2 电路分解
decompose()函数,可以将一个逻辑门分解为指定的一组门。
如:将Tofolli门分解为RX、RZ门。
from pennylane.transforms import decomposefrom functools import partial
dev = qml.device('default.qubit')allowed_gates = {qml.Toffoli, qml.RX, qml.RZ}
@partial(decompose, gate_set=allowed_gates)@qml.qnode(dev)def circuit(): qml.Hadamard(wires=[0]) qml.Toffoli(wires=[0,1,2]) return qml.expval(qml.Z(0))输出结果:
>> print(qml.draw(circuit)())0: ──RZ(1.57)──RX(1.57)──RZ(1.57)─╭●─┤ <Z>1: ───────────────────────────────├●─┤2: ───────────────────────────────╰X─┤8.3 自定义分解逻辑门
通过自定义分解电路,可以将某一个量子逻辑电路中的某一个电路,分解为指定规则的门。
例如:将电路中的所有CNOT门,分解为H门和CZ门。
# 默认电路def circuit(weights): qml.BasicEntanglerLayers(weights, wires=[0, 1, 2]) return qml.expval(qml.Z(0))
# CNOT的转化规则函数def custom_cnot(wires, **_): return [ qml.Hadamard(wires=wires[1]), qml.CZ(wires=[wires[0], wires[1]]), qml.Hadamard(wires=wires[1]) ]
# 可以将一系列规则函数,构成一个列表custom_decomps = {qml.CNOT: custom_cnot}
# 使用自定义的分解方法分解逻辑门。decomp_dev = qml.device("default.qubit", wires=3, custom_decomps=custom_decomps)decomp_qnode = qml.QNode(circuit, decomp_dev)输出结果:
>>> print(qml.draw(decomp_qnode, level="device")(weights))0: ──RX(0.40)────╭●──H───────╭Z──H─┤ <Z>1: ──RX(0.50)──H─╰Z──H─╭●────│─────┤2: ──RX(0.60)──H───────╰Z──H─╰●────┤9. 量子编译流程
9.1 catalyst混合量子程序实时编译器
通过pip安装:
pip install pennylane-catalyst使用@qjit装饰器编译量子程序
from jax import numpy as jnp
dev = qml.device("lightning.qubit", wires=2, shots=1000)
@qml.qjit@qml.qnode(dev)def circuit(params): # 一个量子电路 qml.Hadamard(0) qml.RX(jnp.sin(params[0]) ** 2, wires=1) qml.CRY(params[0], wires=[0, 1]) qml.RX(jnp.sqrt(params[1]), wires=1) return qml.expval(qml.Z(1))@qjit还可以编译混合量子程序。即:同时包括量子电路和经典处理流程的函数。
@qml.qjitdef hybrid_function(params, x): grad = qml.grad(circuit)(params) # 量子电路 return jnp.abs(grad - x) ** 2 # 经典数据处理9.2 控制流程
Catalyst编译器,可以支持使用python中的条件控制来控制量子电路。需要设置参数autograph=True
@qml.qjit(autograph=True) # 设置参数@qml.qnode(dev)def circuit(x: int): # 使用python的控制流 if x < 5: qml.Hadamard(wires=0) else: qml.T(wires=0)
return qml.expval(qml.Z(0))输出结果:
>>> circuit(3)array(0.)>>> circuit(5)array(1.)AutoGraph的使用存在一些限制,见相关文档AutoGraph Guid
10. 使用CUDA Quantum
注:CUDA Quantum 不支持 Catalyst编译器的一些特性,如:AutoGraph,控制流、测量统计信息等。
pip安装CUDA Quantum
pip install pennylane-catalyst cuda_quantum在@qml.qjit装饰器中设置参数:compiler=cuda_quantum。
# 设置设备类型为software.qppdev = qml.device("softwareq.qpp", wires=2)
# 编译器使用CUDA Quantum@qml.qjit(compiler="cuda_quantum")@qml.qnode(dev)def circuit(x): qml.RX(x[0], wires=0) qml.RY(x[1], wires=1) qml.CNOT(wires=[0, 1]) return qml.expval(qml.Y(0))输出结果:
>>> circuit(jnp.array([0.5, 1.4]))-0.47244976756708373CUDA Quantum的设备类型存在限制:
-
softwareq.qpp: a modern C++ statevector simulator -
nvidia.custatevec: The NVIDIA CuStateVec GPU simulator (with support for multi-gpu) -
nvidia.cutensornet: The NVIDIA CuTensorNet GPU simulator (with support for matrix product state)
